Ever since I watched the film “21,” the conundrum of two goats and a car has intrigued me. Despite multiple attempts to grasp the film’s explanation, I remained baffled. That is, until today. Before delving into the details, let me present the problem for those who are unfamiliar.
The Problem: Imagine you’re on a game show with three doors. Behind one door is a car, and behind the other two doors are goats. You choose a door, let’s call it Door 1. The host, who knows where the car is, opens another door, perhaps Door 3, revealing a goat. Now, you have a choice: stick with your original choice (Door 1) or switch to the unopened door (Door 2).
Initially, I struggled to wrap my head around the film’s answer, which was to switch the door. In my mind, both options seemed equally likely. Whether I stuck with my initial choice or switched, the odds of winning the car remained at 1/3.
Allow me to offer an alternative explanation. Let’s consider the three choices: Doors A, B, and C. The probability of selecting any one of them initially provides a 1/3 chance of winning the car. Now, let’s explore the scenarios, keeping in mind that the host will always reveal a goat behind a door you didn’t pick.
Option 1: Choose A, host shows B, you stick with A. Result: You lose.
Option 2: Choose A, host shows B, you switch to C. Result: You win.
Option 3: Choose B, host shows A, you stick with B. Result: You lose.
Option 4: Choose B, host shows A, you switch to C. Result: You win.
Option 5: Choose C, host shows A or B, you stick with C. Result: You win.
Option 6: Choose C, host shows A or B, you switch to A or B. Result: You lose.
Now, imagine that the host asks you whether you want to switch doors. Let’s focus on the switching options: Options 2, 4, and 6. Out of these, you win the car two times, yielding a 2/3 probability. Contrastingly, the cases where you stick with your initial choice Options 1, 3, and 5 provide a 1/3 chance of winning. Hence, the optimal strategy is always to switch.
For a more intuitive grasp, consider this experimental approach: How can we verify if a coin toss yields a 50% chance of heads? We toss it numerous times and count the heads, right? How many tosses are needed to confidently assert a 50% heads probability? 100 times? 1000 times? Let’s say 10,000 times to establish a solid foundation. Now, let’s apply the same principle to our Monty Hall scenario.
Let’s allow our code to handle the task for us, shedding light on how often switching doors secures us the coveted car.
import numpy as np
import matplotlib.pyplot as plt
def monty_hall_simulation(num_samples):
stay_wins = 0
switch_wins = 0
for _ in range(num_samples):
# Assigining car to random door
prize_door = np.random.randint(3)
# Picking a random door
contestant_choice = np.random.randint(3)
# Host reavealing door that does not have car
revealed_door = np.random.choice([door for door in range(3) if door != contestant_choice and door != prize_door])
# Contestant's choice after switching
switch_choice = next(door for door in range(3) if door != contestant_choice and door != revealed_door)
# Check if the contestant wins by staying or switching
stay_wins += contestant_choice == prize_door
switch_wins += switch_choice == prize_door
return stay_wins, switch_wins
def plot_results(stay_wins, switch_wins):
labels = ['Stay', 'Switch']
values = [stay_wins, switch_wins]
plt.bar(labels, values)
plt.xlabel('Strategy')
plt.ylabel('Number of Wins')
plt.title('Monty Hall Problem Simulation')
plt.show()
num_samples = 100000
stay_wins, switch_wins = monty_hall_simulation(num_samples)
plot_results(stay_wins, switch_wins)
print("Won by staying with the choice: {}, Won by switching: {}".format(stay_wins, switch_wins))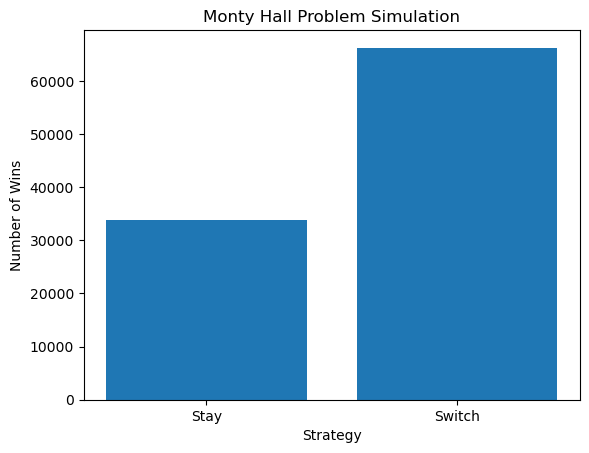
Won by staying with the choice: 33748, Won by switching: 66252
